Alternate Scoring Methods
- Z-Score – compete against your own averages
- Eigenvector Boat Rank – Which boat is best
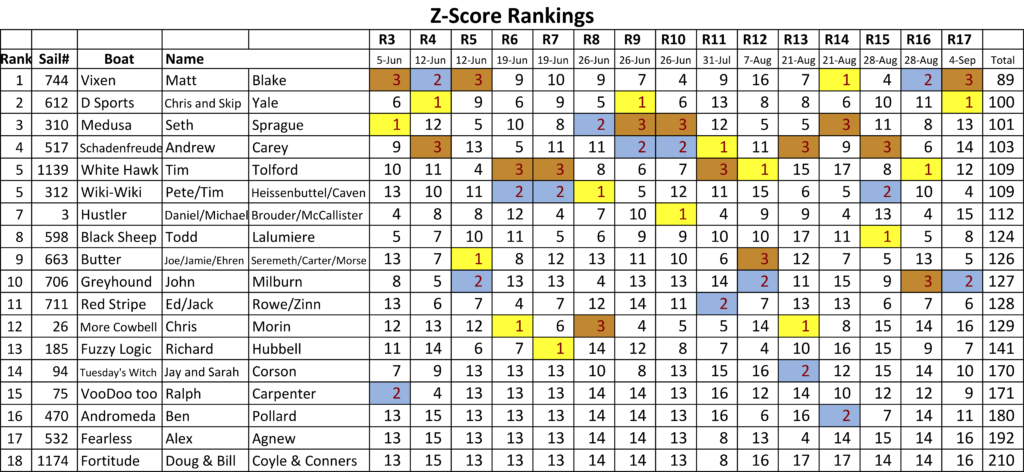
Z-Score Performance Handicap method measures how a competitor does versus his/her own average position. This is an experimental alternate scoring approach developed by Matt Blake. For more discussion, see the Z-Score description. And, if anyone wants to discuss and develop this scoring approach further, please contact Matt.
The table below is the overall 2018 season series tabulation using the rank-order scores based on the normalized z-scores. Any ties are left as ties, and no throw-outs are used. For further information, refer to the z-score description of the scoring system that is presented elsewhere on the website.
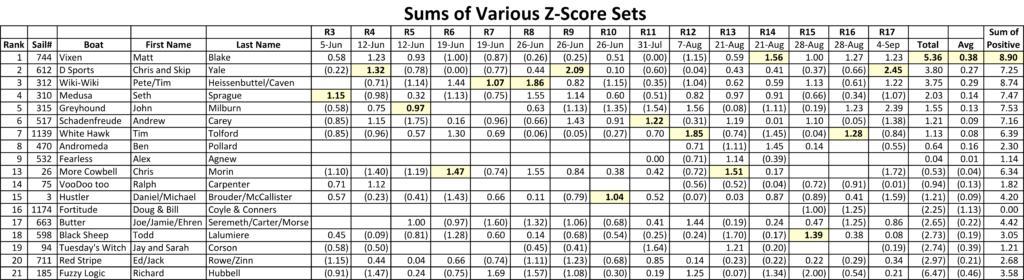
Sums of Various Sets of Z-Scores
Another option is to add up the raw (normalized) z-scores, and rank the fleet according to total score, rather than by individual race ranking. Or, maybe we just add up the positive (better than average) scores and forget about the negative ones. We probably need to try a few alternate approaches to see what works best. Below, the scores are ranked by the sum of the raw z-scores (the sums from only races 3 and on, since races 1 and 2 are initialization races for the z-score and do not really have much meaning here). Blank cells are races not sailed, DSQ’d, etc. Negative numbers (for races worse than the boat’s average) are enclosed in parenthesis (i.e., accountant’s formatting).
The average of the z-scores looks like a another possible choice for scoring a series, as shown below. The total z-score is averaged by the number of races actually sailed.
If the scores are the sum of positive z-scores (i.e., only those score better than the boat’s average), the series results are as shown in the table below.
Top 3 Finishers Under The Z-Score Performance Handicap Rule
September 4 – Race #1 (17th race of 2018 season):
- D Sports (2.45 pts)
- Greyhound (2.39 pts)
- Vixen (1.23 pts)
August 28 – Race #2 (16th race of 2018 season):
- Vixen (1.28 pts)
- White Hawk (1.27 pts)
- Greyhound (1.23 pts)
August 28 – Race #1 (15th race of 2018 season):
- Black Sheep (1.39 pts)
- Wiki Wiki (1.15 pts)
- Schadenfreude (1.10 pts)
August 21 – Race #2 (14th race of 2018 season):
- Vixen (1.60 pts)
- Medusa (0.91 pts)
- Hustler (0.84 pts)
August 21 – Race #1 (13th race of 2018 season):
- More Cowbell (1.51 pts)
- Tuesday’s Witch (1.21 pts)
- Schadenfreude (1.19 pts)
August 7 – Race #1 (12th race of 2018 season):
- White Hawk (1.76 pts)
- Greyhound (1.43 pts)
- Butter (1.41 pts)
July 31 – Race #1 (11th race of 2018 season):
- Schadenfreude (1.22 pts)
- Red Stripe (0.85 pts)
- White Hawk (0.65 pts)
June 26 – Race #3 (10th race of 2018 season):
- Hustler (1.00 pts)
- Schadenfreude (0.93 pts)
- Medusa (0.62 pts)
June 26 – Race #2 (9th race of 2018 season):
- D-Sports (2.03 pts)
- Schadenfreude (1.45 pts)
- Medusa (1.13 pts)
June 26 – Race #1 (8th race of 2018 season):
- Wiki Wiki (2.92 pts)
- More Cowbell (1.59 pts)
- Medusa (1.52 pts)
June 19 – Race #2 (7th race of 2018 season):
- Fuzzy Logic (1.67 pts)
- Wiki Wiki (1.07 pts)
- White Hawk (0.63 pts)
June 19 – Race #1 (6th race of 2018 season):
- More Cowbell (1.48 pts)
- Wiki Wiki (1.45 pts)
- White Hawk (1.30 pts)
June 12 – Race #2 (5th race of 2018 season):
- Greyhound (1.14 pts)
- Butter (1.00 pts)
- Vixen (0.96 pts)
June 12 – Race #1 (4th race of 2018 season):
- Vixen (1.29 pts)
- D-Sports (1.25 pts)
- VooDoo too & Schadenfreude (1.12 pts)
June 5 – Race #2 (3rd race of 2018 season):
- Medusa (1.14 pts)
- VooDoo (0.71pts)
- Hustler & Vixen (0.58 pts)
Top Gun – Which boat showed the most skill in 2018? NEWLY UPDATED 12/12/18
If we eliminate the scoring benefit accrued to the boats that did Race Committee duty, and do not penalize boats that do not come to the start the way that low-point scoring does, but look only at boat-against-boat results and only at each boat’s races where the boat actually finished, the following table gives a ranking for the best performing racers over the season. There is some eigenvector mathematics behind this table that is similar to Google’s page ranking methodology used to select the search results that are displayed on your computer screen.
The goal is to rank the fleet in the order of each boat’s likelihood of beating the other boats in a race. A remaining issue is how best to “normalize” the boat-to-boat wins so that a boat that sails more races does not benefit compared to a boat with fewer races. We have settled on normalizing the boat-to-boat wins by the pairings to compute the “pairings win percentage”, although we have looked at normalizing by the number of races a boat completes, as well as the length of the “win vector.”
The way the eigenvector mathematics work in this scoring method is a boat derives its score by beating other boats (based on one-on-one comparisons to each other boat within each race). A boat scores nothing for each loss to another boat and it scores nothing for not finishing (or competing). Furthermore, the score a boat achieves is also dependent on how good the boat it beats is — beating a boat higher in the standings scores better than beating a boat lower in the standings. Thus, the top boats get a double benefit by beating a lot of other boats, and by beating better boats. Finally, a boat’s results are normalized to prevent a boat from dominating just by showing up to all the races. The corollary to this is that a boat that shows up for just a few races can win the series under this scoring method if it beats all the other boats when it does show up. The bottom line is that this scoring method ranks the boats from best to worst racing skill level, the “best” defined by a boat’s measured ability to beat the best competitors.
The summary table of results provided below includes, on the left, the ranking and raw scores using this new method, and in the middle, the ranking and scores using the standard RRS Appendix A9 low-point scoring method. On the far right column, the change in position from the standard RRS A9 rankings (+1 means improve 1 place from our standard scoring method).
Thank you to Dr. Eric Arens of Richmond Yacht Club of California for the insight to adapt Google’s PageRank technique and for assistance with the eigenvector mathematics.
BoatRank© Eigensolver Results for 2018
| Position Calculated by Boat Rank | Boat Sail No. | Raw Score | RRS A9 Position | RRS Net Score | Change in Overall Position |
|---|---|---|---|---|---|
| 1 | 744 | 0.380 | 1 | 40.8 | 0 |
| 2 | 517 | 0.356 | 2 | 46 | 0 |
| 3 | 3 | 0.353 | 3 | 47.8 | 0 |
| 4 | 711 | 0.349 | 4 | 50.6 | 0 |
| 5 | 1139 | 0.336 | 5 | 53.4 | 0 |
| 6 | 26 | 0.247 | 8 | 89 | 2 |
| 7 | 310 | 0.228 | 6 | 82 | -1 |
| 8 | 185 | 0.227 | 7 | 87.2 | -1 |
| 9 | 598 | 0.221 | 9 | 91 | 0 |
| 10 | 663 | 0.206 | 10 | 109.8 | 0 |
| 11 | 312 | 0.155 | 11 | 123.6 | 0 |
| 12 | 470 | 0.152 | 16 | 216.5 | 4 |
| 13 | 706 | 0.132 | 13 | 129 | 0 |
| 14 | 612 | 0.123 | 12 | 129 | -2 |
| 15 | 1174 | 0.106 | 19 | 268.4 | 4 |
| 16 | 315 | 0.102 | 18 | 261 | 2 |
| 17 | 75 | 0.082 | 14 | 203 | -3 |
| 18 | 532 | 0.075 | 17 | 250 | -1 |
| 19 | 94 | 0.004 | 15 | 207 | -4 |
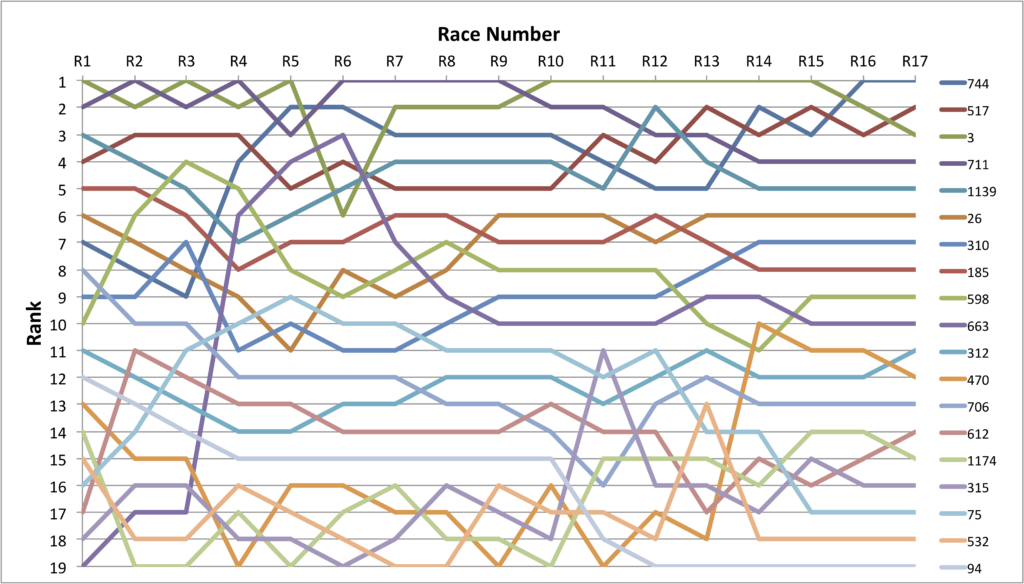
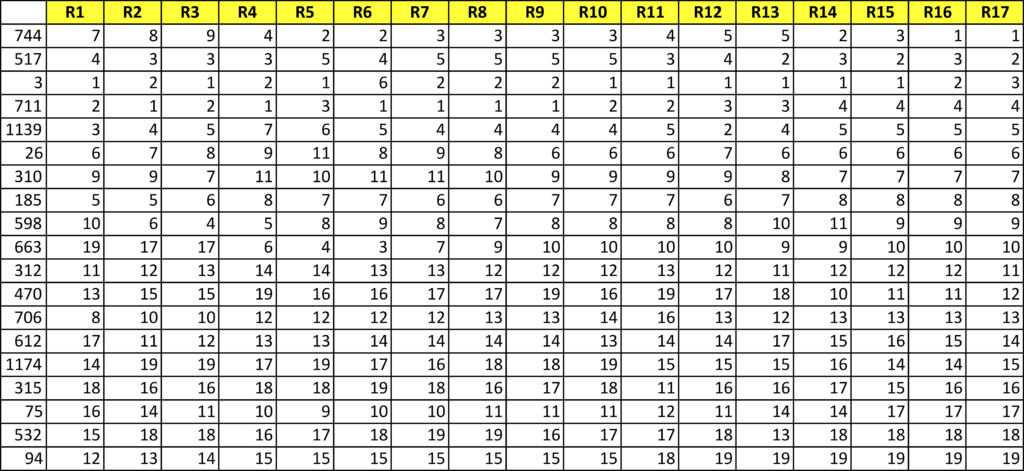
Season Rankings by BoatRank©
With a little more calculation, the chart and table below provide the race-by-race progression of cumulative ranking (i.e., at the end of each race) using this scoring approach. These results are now updated to “normalize” each boats race results over the series.